Konkursowi patronują:
W serwisie Kangur Matematyczny wykorzystywane są pliki cookies do przechowywania informacji o zalogowanych użytkownikach oraz do zbierania statystyk odwiedzin i badania natężenia ruchu na stronie. Jeśli nie wyrażasz zgody na wykorzystywanie plików cookies, to zmień ustawienia swojej przeglądarki internetowej.





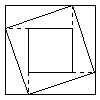
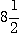 cm2
cm2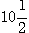 cm2
cm2