Niech N będzie najmniejszą liczbą naturalną o sumie cyfr równej 2019. Jaka jest pierwsza od lewej cyfra liczby N?

Ze zbioru wierzchołków pewnego wielokąta wypukłego wybieramy losowo dwa punkty. Prawdopodobieństwo, że wybrane punkty są końcami pewnej przekątnej tego wielokąta, wynosi 0,8. Ile boków ma wielokąt?

Cztery różne proste przechodzące przez początek układu współrzędnych przecinają parabolę y = x² − 2 w ośmiu punktach. Czemu może być równy iloczyn odciętych (tj. współrzędnych „iksowych”) tych ośmiu punktów?

W pudełku jest 65 kul, przy czym 8 z nich jest białych, a pozostałe są czarne. W jednym ruchu możemy wyjąć z pudełka nie więcej niż 5 kul. Kule raz wyjęte z pudełka już do niego nie wracają. Jaką najmniejszą liczbę ruchów trzeba wykonać, aby mieć pewność, że została wyjęta przynajmniej jedna biała kula?

Spośród pięciu kart oznaczonych liczbami 3, 4, 5, 6 i 7 Anna wybrała trzy, a Beata dostała pozostałe dwie. Każda z nich obliczyła iloczyn liczb na swoich kartach i okazało się, że suma tych iloczynów jest liczbą pierwszą. Ile wynosi suma liczb na kartach Anny?

Czterej bracia A, B, C i D są różnego wzrostu. Oświadczyli oni, co następuje. A powiedział: ,,Nie jestem ani najniższy, ani najwyższy'', B: ,,Nie jestem najniższy'', C: ,,Jestem najwyższy'', a D~powiedział: ,,Jestem najniższy''. Który z nich jest najwyższy, jeśli dokładnie jeden z nich skłamał?

Bartek jest zapalonym modelarzem. Jego ulubionym modelem jest model kolejki elektrycznej w skali 1 : 87 zwany przez modelarzy H0. Wykonał do niego wiele dodatkowych figurek, w tym dwucentymetrową figurkę swojego brata, oczywiście wszystkie w skali modelu. Jaki jest rzeczywisty wzrost jego brata?

Wynalazca Klapaucjusz skonstruował robota obdarzonego sztuczną inteligencją. Niestety w wyniku błędu w programie w każdych trzech kolejnych wypowiadanych przez niego zdaniach jest dokładnie jedno fałszywe. Robot poproszony o podanie własności pewnej liczby dwucyfrowej powiedział w kolejności: „Jedną z jej cyfr jest 2”, „Jest większa niż 50”, „Jest parzysta”, „Jest mniejsza niż 30”, „Jest podzielna przez 3”, „Jedną z jej cyfr jest 7”. Ile jest równa suma cyfr tej liczby?

Długości wszystkich boków trójkąta prostokątnego są liczbami naturalnymi. Jaki jest obwód tego trójkąta, jeśli jedna z przyprostokątnych ma długość 29?

Kacper i Melchior mają razem 35 lat, Melchior i Baltazar mają razem 36 lat, a Baltazar i Kacper mają razem 37 lat. Ile lat ma najstarszy z nich?

Wyspę Laputa zamieszkują wyłącznie Matematycy -- którzy zawsze mówią prawdę, i Krętacze -- którzy zawsze kłamią. W czasie swoich podróży dr~Guliwer spotkał \mat{7} mieszkańców tej wyspy siedzących wokół okrągłego stołu. Każdy z nich powiedział: Siedzę pomiędzy dwoma Krętaczami. Ilu Krętaczy siedziało przy tym stole?

Liczba pierwsza p dzieli sumę wszystkich liczb naturalnych od 1 do n, ale nie dzieli żadnego ze składników tej sumy. Która z następujących liczb może być równa sumie n+p?

Piotr dodał do siebie 31 kolejnych liczb naturalnych od 2001 do 2031, a następnie otrzymaną sumę podzielił przez 31. Jaki wynik otrzymał?

Sprzedawca samochodów nabył dwa samochody, a następnie odsprzedał je swoim klientom. Pierwszy samochód sprzedał za cenę o 40% wyższą od ceny zakupu, a drugi samochód sprzedał za cenę o 60% wyższą od ceny jego zakupu. W sumie za oba samochody zainkasował o 54% więcej, niż wydał na ich zakup. Jaki jest stosunek ceny, za jaką sprzedawca nabył pierwszy samochód, do ceny, za jaką nabył drugi samochód?

Protazy i Gerwazy – każdy na swój sposób – zamienili litery słowa KANGAROO cyframi, otrzymując ośmiocyfrowe liczby podzielne przez 11. Każdy z nich zastąpił różne litery różnymi cyframi, a takie same litery – równymi cyframi. Gerwazy otrzymał największą możliwą liczbę, a Protazy – najmniejszą. Okazało się, że obaj zastąpili pewną literę tą samą cyfrą. Jaka to cyfra?

Kacper, Melchior i Baltazar obchodzą dziś urodziny. Kacper dodał lata, które każdy z nich ukończył i otrzymał liczbę 44. Po pewnym czasie suma ich lat będzie znowu liczbą dwucyfrową o~równych cyfrach. Jaka to liczba?

Dla jakiego n sześć tygodni to dokładnie 1⋅2⋅3⋅4⋅…⋅n sekund?

W lasach jednej z wysp Archipelagu Bergamutów żyją trzy rodzaje zwierząt: sarny, wilki i lwy. Wilki zjadają sarny, lwy zjadają zarówno sarny jak i wilki. Gdy wilk zje sarnę, zmienia się w lwa. Gdy lew zje sarnę, zmienia się w wilka, a gdy zje wilka, zmienia się w sarnę. Początkowo na wyspie było 17 saren, 55 wilków i 6 lwów. Jaka jest największa możliwa liczba zwierząt, które mogą pozostać na tej wyspie w sytuacji, gdy żadne zwierzę nie może zjeść innego?

Sześciu herosów pojmało 20 łotrów. Pierwszy heros pojmał jednego łotra, drugi dwóch, a trzeci trzech. Czwarty heros pojmał więcej łotrów niż którykolwiek z pozostałych pięciu. Najmniejsza możliwa liczba łotrów pojmanych przez czwartego herosa jest równa

Rozważmy prostokąty, których jeden z boków ma długość 5 i które mają tę własność, że można je podzielić na prostokąt i kwadrat, przy czym któraś z tych figur ma pole równe 4. Ile nieprzystających prostokątów ma tę własność?

Na wyspach Bergamutach żyją dwa typy mieszkańców: prawdomówni - którzy zawsze mówią prawdę, i kłamcy - którzy zawsze kłamią. Po przybyciu na te wyspy spotkałem dwóch Bergamutan: wysokiego i niskiego. Zapytałem wysokiego, czy obaj są prawdomówni, ale z odpowiedzi nie mogłem wywnioskować, kim oni byli. Wówczas zapytałem niskiego, czy wysoki jest prawdomównym, a gdy odpowiedział, wiedziałem już, do jakiego typu należał każdy z nich. Kim byli napotkani Bergamutanie?

Mój wiek wyraża się liczbą dwucyfrową, która jest potęgą o wykładniku naturalnym liczby 5. Wiek mojego kuzyna wyraża się liczbą dwucyfrową, która jest potęgą o wykładniku naturalnym liczby 2. Łączna suma cyfr dwóch liczb wyrażających mój wiek i wiek mojego kuzyna jest nieparzysta. Ile jest równy iloczyn wszystkich cyfr obu tych liczb?

Biuro podróży zaproponowało grupie turystów zwiedzających Warmię i Mazury cztery opcjonalne oferty dodatkowych atrakcji. Z każdej z tych ofert skorzystało 80% członków grupy. Z wszystkich czterech ofert skorzystało p procent członków grupy. Najmniejszą wartością p, przy której jest to możliwe, jest

Każda z pięciu lamp układu jest w jednym z dwóch stanów: albo "świeci", albo "nie świeci". Każdorazowe naciśnięcie włącznika dowolnej lampy zmienia stan tej lampy i jeszcze jednej losowo wybranej lampy spośród pozostałych (nie musi to być za każdym razem ta sama lampa). Na początku wszystkie lampy były w stanie "nie świeci". Włączniki tego układu lamp naciśnięto dokładnie 10 razy. Wówczas na pewno:

Dwaj bracia, Gerwazy i Protazy, udzielili prawdziwych odpowiedzi na pytanie o liczbę członków klubu dyskusyjnego, do którego należą. Gerwazy powiedział: Wszyscy członkowie naszego klubu, oprócz pięciu, są płci męskiej. Protazy powiedział: Wśród dowolnie wybranych sześciu członków naszego klubu są zawsze co najmniej cztery panie. Ilu członków liczy ten klub dyskusyjny?

48 chłopców wybrało się na wspólną wyprawę narciarską. Sześciu z nich przybyło z dokładnie jednym bratem, dziewięciu z dokładnie dwoma braćmi i czterech z dokładnie trzema braćmi. Pozostali chłopcy przybyli bez rodzeństwa. Z ilu rodzin było tych 48 chłopców?

Sześcian o wymiarach 3×3×3 jest zbudowany z 27 identycznych sześcianików o wymiarach 1×1×1. Ile takich sześcianików przecina płaszczyzna prostopadła do przekątnej sześcianu i przechodząca przez jego środek?

Mam dwa naczynia w kształcie sześcianu: jedno o polu podstawy 4 dm², drugie o polu podstawy 1 dm². Zamierzam napełnić duże naczynie wodą ze strumienia, używając do tego mniejszego naczynia. Ile co najmniej razy muszę pójść do strumienia, aby napełnić większe naczynie?

W torbie są kule: niebieskie, zielone i czerwone. Wiadomo, że jeżeli losowo wyjmiemy z tej torby pięć kul, to na pewno wśród nich będą co najmniej dwie czerwone i co najmniej trzy będą w tym samym kolorze. Ile kul w tej torbie jest koloru niebieskiego?

E) Nie można tego stwierdzić bez dodatkowych informacji.

Do tablicy, na której wypisano liczby od 1 do 10, podchodzili kolejno uczniowie i każdy z nich zmazywał dwie dowolnie wybrane liczby, a na tablicy zapisywał ich sumę pomniejszoną o 1. W pewnym momencie na tablicy pozostała tylko jedna liczba. Liczba ta

Dany jest wielokąt foremny o 41 kątach. Na ile sposobów można wybrać trzy wierzchołki tego wielokąta, aby utworzyły one trójkąt prostokątny?

Ambroży i Bonifacy biegają wokół stadionu, każdy ze stałą prędkością. Ambroży, który biegnie szybciej niż Bonifacy, okrąża stadion w czasie 3 minut. Obaj wystartowali jednocześnie, z tego samego punktu i w tym samym kierunku. Po upływie 8 minut Ambroży po raz pierwszy zdublował Bonifacego. W jakim czasie Bonifacy pokonuje jedno okrążenie?

W konkursie matematycznym uczestniczyło 55 uczniów. Jurorzy sprawdzający zadania stawiali przy każdym poprawnie rozwiązanym zadaniu znak "+", przy każdym niepoprawnie rozwiązanym zadaniu znak "-", a znak "0", gdy uczestnik zadanie pominął. Po zakończeniu konkursu okazało się, że każde dwie prace różnią się liczbą znaków "+" lub liczbą znaków "-". Jaka jest najmniejsza liczba zadań, przy której jest to możliwe?

Ile liczb pierwszych p ma tę własność, że p⁴+1 też jest liczbą pierwszą?

Dwa okręgi o promieniach 13 i 15 przecinają się w dwóch punktach. Cięciwa łącząca te punkty ma długość 24. Która z poniższych liczb może wyrażać odległość środków tych okręgów przy pewnym ich położeniu?

Kasia dostała w prezencie 36 drewnianych kangurków i pomalowała je, używając trzech kolorów: białego, brązowego i czarnego. Niektóre kangurki pomalowała tylko jednym kolorem, inne dwoma, a pozostałe 5 kangurków wszystkimi trzema kolorami. Białej farby użyła do pomalowania 25 kangurków, brązowej do pomalowania 28 kangurków, a czarnej do pomalowania 20 kangurków. Ile kangurków pomalowała tylko jednym kolorem?

Michał na egzaminie testowym odpowiedział poprawnie na 80% pytań, a na pozostałe 5 pytań nie udzielił odpowiedzi. Ile było pytań w teście?

Pewna wyspa zamieszkana jest wyłącznie przez kłamców i przez rycerzy. Każdy kłamca zawsze kłamie, każdy rycerz zawsze mówi prawdę. Wyspiarz Abacki, zapytany, kim jest on i kim jest jego sąsiad Babacki, odpowiedział: Przynajmniej jeden z nas jest kłamcą. Które z poniższych zdań jest prawdziwe?

Andrzej, Mietek i Zbyszek rzucają kolejno kostką do gry. Andrzej wygrywa, jeżeli wyrzuci 1, 2 lub 3. Mietek wygrywa, jeżeli wyrzuci 4 lub 5. Zbyszek wygrywa, jeżeli wyrzuci 6. Najpierw kostką rzuca Andrzej, potem Mietek, potem Zbyszek, potem znowu Andrzej, znowu Mietek, itd. Gra się kończy, gdy któryś z nich wygra. Jakie jest prawdopodobieństwo, że wygra Zbyszek?

Dwa pociągi równej długości przejeżdżają obok siebie w przeciwnych kierunkach. Pierwszy z nich jedzie z prędkością 100 km/h, drugi z prędkością 120 km/h. Pasażer drugiego pociągu stwierdził, że pierwszy pociąg mijał go przez 6 sekund. Ile sekund mijał drugi pociąg stojącego przy oknie pasażera pierwszego pociągu?

Reszta z dzielenia liczby 1001 przez pewną liczbę jednocyfrową jest równa 5. Ile wynosi reszta z dzielenia 2006 przez tę samą liczbę jednocyfrową?

Paweł wybrał jedną liczbę z pewnego ciągu dziesięciu kolejnych liczb naturalnych. Suma pozostałych dziewięciu liczb tego ciągu jest równa 2006. Jaką liczbę wybrał Paweł?

Na płaszczyźnie dane są punkty P i Q, przy czym |PQ|=5. Ile istnieje na tej płaszczyźnie trójkątów, których jednym z boków jest odcinek PQ i których boki mają długości: 3, 4 i 5?

W trzech pudełkach jest razem 60 kart. Gdyby wszystkie karty z pierwszego pudełka przełożyć do drugiego pudełka, w pudełku tym byłoby dwa razy więcej kart niż w trzecim pudełku. Gdyby zaś wszystkie karty z trzeciego pudełka przełożyć do drugiego pudełka, w pudełku tym byłoby trzy razy więcej kart niż w pierwszym pudełku. Ile kart było w drugim pudełku?

Ada co drugi dzień mówi wyłącznie prawdę, w pozostałe dni wyłącznie kłamie. Dziś wypowiedziała dokładnie cztery z pięciu poniższych zdań. Którego z nich nie wypowiedziała?

Ile wierzchołków ma wielokąt foremny, w którym suma kątów wewnętrznych jest siedem razy mniejsza niż suma kątów 16-kąta foremnego?

Ile istnieje kwadratów na płaszczyźnie Oxy, których jednym z wierzchołków jest punkt A(-1,-1) i których osią symetrii jest przynajmniej jedna z osi układu współrzędnych?

Dany jest ciąg liczbowy składający się z dwustu zer. Przekształcamy ten ciąg w inny ciąg dwustuelementowy w następujący sposób: W pierwszym etapie dodajemy do każdego wyrazu ciągu liczbę 1. W drugim etapie dodajemy do każdego wyrazu o numerze parzystym otrzymanego w pierwszym etapie ciągu liczbę 1. W trzecim etapie dodajemy do każdego wyrazu o numerze podzielnym przez trzy otrzymanego w drugim etapie ciągu liczbę 1, itd. Po 200 etapach otrzymamy ciąg, którego 120. wyraz będzie równy:

Liczby 15, 13, 12 są odpowiednio długościami dwóch boków trójkąta ostrokątnego i wysokości opuszczonej na trzeci bok. Jakie jest pole tego trójkąta?

Ile wyrazów ciągu, którego wyrazami są siódme potegi kolejnych liczb naturalnych, znajduje się między liczbami 5²¹+1 i 2⁴⁹-1?

W kole o promieniu 15 obrano punkt P odległy od środks koła o 9. Ile istnieje różnych cięciw przechodzących przez punkt P, których długości wyrażają się liczbami całkowitymi?

W pewnym hotelu w ciągu trzech letnich miesięcy zajętych jest średnio 88% pokoi, w pozostałych dziewięciu miesiącach roku zajętych jest średnio 64% pokoi. Ile średnio pokoi jest zajętych w ciągu całego roku?

Na płaszczyźnie dany jest zbiór A składający się z dziesięciu punktów. Dokładnie pięć z nich leży na pewnej prostej i żadna inna prosta nie zawiera więcej niż dwa spośród tych dziesięciu punktów. Ile można utworzyć trójkątów o wierzchołkach należących do zbioru A?

Ile istnieje nieprzystających trójkątów utworzonych przez wierzchołki ośmiokąta foremnego?

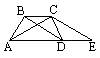Na rysunku obok BC || AE, BD || CE. Jeżeli x oznacza pole czworokąta ABCD, y zaś pole trójkąta ACE, to

W turnieju piłki nożnej wzięły udział drużyny A, B, C i D. W każdym meczu drużyna zwycięska otrzymuje 3 punkty, przegrana 0 punktów, za remis obie drużyny otrzymują po jednym punkcie. Każda drużyna rozegrała z każdą inną dokładnie jeden mecz. Wyniki końcowe były następujące: drużyna A zdobyła 7 punktów, B - 4 punkty, C - 3 punkty, D - 3 punkty. Jak zakończył się mecz pomiędzy drużynami A i D?

Wujek Antoni złowił pewną liczbę ryb. Trzy największe spośród nich dał cioci Halinie, w wyniku czego waga złowionych ryb zmalała o 35%. Następnie trzy najmniejsze ryby dał sąsiadowi, zmniejszając wagę pozostałych ryb o . Ile ryb złowił wujek Antoni?

Statek kosmiczny leci z Ziemi do odległej o 2²⁰ km planety X. Gdy statek przebył ¹/₄ drogi, utracił kontakt radiowy z Ziemią. Kontakt ten odzyskał w odległości 2¹⁹ km od Ziemi. Ile kilometrów leciał bez kontaktu radiowego?

Bartosz powinien pomnożyć dwie dwucyfrowe liczby naturalne. Niestety, pomylił się i przemnożył pierwszą z nich przez liczbę powstałą przez zamianę kolejności cyfr liczby drugiej. Otrzymany wynik był o 3816 większy od właściwego. Jaki powinien być właściwy wynik?

Jeżeli p(n) oznacza iloczyn cyfr liczby naturalnej n, to p(1)+p(2)+p(3)+...+p(100) jest równe

Kurs dolara w trzech kantorach wymiany walut był wczoraj rano taki sam. Następnie w pierwszym z nich kurs ten wzrósł przed południem o 1%, a po południu zmalał o 1%. W drugim przed południem kurs zmalał o 1%, a po południu wzrósł o 1%. W trzecim kantorze kurs nie ulegał zmianom. W którym z tych kantorów kurs dolara był pod koniec wczorajszego dnia najwyższy?

Okrągły stół o średnicy 2 m przykryty został cienkim kwadratowym obrusem o długości boku 2,5 m. Środek blatu stołu pokrywa się ze środkiem obrusa. Jaka jest różnica pomiędzy odległościami od podłogi najniżej i najwyżej położonego punktu na brzegu obrusa?

Na pewnej wyspie mieszkają wyłącznie ludzie albo prawdomówni - zawsze mówiący prawdę, albo kłamcy - zawsze kłamiący. Liczba wszystkich mieszkańców tej wyspy wynosi 1999. Każdy z nich ma dokładnie jedną pasję: albo lubi śpiewać, albo grać w piłkę nożną, albo łowić ryby. Każdemu z mieszkańców wyspy zadano trzy pytania:

1. Czy lubi śpiewać?
2. Czy lubi grać w piłkę nożną?
3. Czy lubi łowić ryby?

Na pierwsze pytanie odpowiedzi twierdzącej udzieliło 1000 osób, na drugie 700 osób i na trzecie 500 osób. Ilu kłamców mieszka na tej wyspie?

Dwa różne wielomiany f(x)=x²+ax+b i g(x)=x²+cx+d spełniają warunek f(19)+f(98)=g(19)+g(98). Ile rozwiązań ma równanie f(x)=g(x)?

Dziadek ma więcej niż 50, ale mniej niż 70 lat. Każdy z jego synów (dziadek nie ma córek) ma tyle samo synów ilu braci. Suma liczby synów i liczby wnuków jest równa wiekowi dziadka. Ile lat ma dziadek i ilu ma on wnuków?

Jeżeli długość pewnej środkowej w trójkącie jest równa promieniowi okręgu opisanego na tym trójkącie, to ten trójkąt jest