Liczba jest mniejsza od swojej połowy i większa od swojej dwukrotności. Suma tej liczby i jej kwadratu jest równa zero. Co to za liczba?

W pewnej rodzinie jest dokładnie sześciu braci, których wiek w latach tworzy ciąg kolejnych liczb naturalnych. Każdemu z braci zadano pytanie: ,,Ile lat ma najstarszy z twoich braci?'' Wszyscy udzielili prawidłowych odpowiedzi. Która z poniższych liczb nie może być sumą liczb ze wszystkich odpowiedzi?

Litewski książę Jagiełło, po przybyciu w 1386 r. do Krakowa, rozdzielił pomiędzy towarzyszącą mu świtę 200 złotych monet i 600 srebrnych. Każdy rycerz otrzymał 5 złotych monet i 10 srebrnych. Każdy giermek otrzymał 3 złote monety i 8 srebrnych monet. Każdy paź otrzymał 1 złotą monetę i 6 srebrnych. Ile osób zostało obdarowanych?

Po pierwszej połowie meczu piłki ręcznej drużyna gości prowadziła wynikiem 9:14. W drugiej połowie gospodarze zdobyli 2 razy więcej bramek niż goście i ostatecznie wygrali mecz z przewagą jednej bramki. Jaki był końcowy wynik tego meczu?

Gdy podzielimy z resztą liczbę 2021 przez którąkolwiek z liczb 6, 7, 8, 9, to otrzymamy resztę równą 5. Ile jest liczb całkowitych dodatnich mniejszych od 2021 o tej własności?

Krystyna ma osiem monet, których wagi w gramach są różnymi liczbami całkowitymi. Gdy Krystyna położy na lewej szalce wagi dowolne dwie monety, a na prawej szalce dowolne inne dwie monety, to zawsze cięższą stroną jest ta, na której leży najcięższa z tych czterech monet. Co najmniej ile gramów waży najcięższa z tych ośmiu monet?

Kim jest dla Kasi mama córki Kasi babci?

Jeżeli 17x+51y=102, to 9x+27y=

Każda z ośmiu kolejnych trzycyfrowych liczb naturalnych dzieli się przez swoją cyfrę jedności. Ile wynosi suma cyfr najmniejszej z tych ośmiu liczb?

Waga każdego z trzech kangurów wyraża się całkowitą liczbą kilogramów, przy czym liczby te są parami różne. Łącznie kangury te ważą 97 kilogramów. Co najwyżej ile waży najlżejszy z nich?

60 jabłek i 60 gruszek mamy włożyć do skrzynek w taki sposób, że w każdej skrzynce będzie ta sama liczba jabłek i w żadnych dwóch skrzynkach nie będzie tej samej liczby gruszek. Ile jest równa możliwie największa liczba skrzynek, w których możemy rozmieścić te owoce w opisany sposób?

W wierzchołki kwadratu wpisujemy liczby naturalne w taki sposób, że jedna z dwóch liczb wpisanych w końce dowolnego boku kwadratu dzieli drugą, żadna zaś z dwóch liczb wpisanych w końce przekątnych tego kwadratu nie dzieli drugiej. Ile wynosi możliwie najmniejsza suma czterech liczb wpisanych w wierzchołki w taki sposób?

W pewnej rodzinie każde dziecko ma przynajmniej dwóch braci i przynajmniej jedną siostrę. Co najmniej ile dzieci jest w tej rodzinie?

Zosia chciała kupić wymarzoną książkę, ale nie miała żadnych pieniędzy. Zrealizowała swoje marzenie z pomocą ojca i swoich dwóch braci, którzy dali jej kwotę potrzebną na zakup. Ojciec dał jej połowę kwoty, którą dostała od swoich braci. Starszy brat dał jej jedną trzecią kwoty, którą dostała od ojca i młodszego brata. Od młodszego brata otrzymała 10 złotych. Ile złotych kosztowała ta książka?

Pewnego dnia każdy z 40 pociągów wykonuje jeden kurs pomiędzy pewnymi dwoma miastami spośród pięciu miast M, N, O, P i R. Dziesięć z tych pociągów wykonuje kurs do M albo z M. Dziesięć z tych pociągów wykonuje kurs do N albo z N. Dziesięć z tych pociągów wykonuje kurs do O albo z O. Dziesięć z tych pociągów wykonuje kurs do P albo z P. Ile pociągów wykonuje kurs do R albo z R?

Dziewczęta trzymając się za ręce tańczą w kręgu. Alicja jest piąta na lewo od Beaty i ósma na prawo od niej. Ile dziewcząt tańczy w tym kręgu?

W czasie wakacji padało 7 razy, zawsze albo rano, albo po południu. Jeśli padało rano, to po południu nie padało. Jeśli padało po południu, to tego dnia rano nie padało. W czasie wakacji było 5 bezdeszczowych poranków i 6 bezdeszczowych popołudni. Co najmniej ile dni trwały te wakacje?

Trzydzieści tancerek ustawiło się w kręgu twarzami skierowanymi do jego środka. Na hasło „Zwrot!” niektóre z tancerek obróciły się w lewo, a wszystkie pozostałe w prawo. Tancerki, które stanęły twarzą w twarz, powiedziały „Cześć”. Okazało się, że takich tancerek było 10. Następnie na hasło „Półobrót!” wszystkie tancerki wykonały pół obrotu i znów te, które stanęły twarzą w twarz, powiedziały „Cześć”. Ile tancerek powiedziało „Cześć” tym razem?

Na ścianach sześciennej kostki widnieją liczby: -1, -3, -5, 2, 4 i 6, po jednej na każdej ścianie. Suma liczb wyrzuconych przy jednoczesnym rzucie dwiema takimi kostkami nie może być równa

Liczby 1, 2, 4, 8, 16, 32, 64, 128 zapisano na 8 kartkach, po jednej na kartce. Alicja wzięła kilka z tych kartek. Pozostałe zabrała Beata. Okazało się, że suma liczb na kartkach zabranych przez Alicję jest o 31 większa od sumy liczb na kartkach Beaty. Ile kartek wzięła Alicja?

Wokół okrągłego stołu usiadły cztery osoby, z których każda uprawia jedną i tylko jedną dyscyplinę sportową: jeździectwo, kolarstwo, łyżwiarstwo, narciarstwo. Osoba jeżdżąca konno siedzi obok Anety po jej lewej stronie. Osoba jeżdżąca na rowerze siedzi naprzeciw Bogdana. Ewa i Filip siedzą obok siebie. Obok osoby jeżdżącej na łyżwach po jej lewej stronie siedzi kobieta. Jaką dyscyplinę sportową uprawia Ewa?

W klasie jest 33 uczniów. Każdy z nich lubi informatykę lub wychowanie fizyczne. Trzech uczniów lubi oba te przedmioty. Liczba uczniów lubiących tylko informatykę jest dwa razy większa od liczby uczniów lubiących tylko wychowanie fizyczne. Ilu uczniów tej klasy lubi informatykę?

Każdy mieszkaniec planety X ma przynajmniej 2 czułki. Trzech mieszkańców tej planety o imionach: Imi, Dimi i Trimi spotkało się w kraterze. Imi powiedział: „Widzę 8 czułków”, Dimi: „Widzę 7 czułków”, a Trimi: „Widzę tylko 5 czułków”. Żaden z nich nie mógł widzieć swoich czułków. Ile czułków ma Trimi?

Rowerzysta przejechał ze stałą prędkością dystans 84 km. W ciągu godziny jazdy pokonywał dystans o 2km dłuższy od zaplanowanego, co skróciło planowany czas całego przejazdu o 1 godzinę. Z jaką prędkością jechał rowerzysta?

Na płaszczyźnie z układem współrzędnych Tomek narysował kwadrat. Jedna z jego przekątnych ma końce w punktach o współrzędnych (-1,0) i (5,0). Jeden z dwóch pozostałych wierzchołków kwadratu ma współrzędne

Piechur przeszedł dystans 8 km ze stałą prędkością 4 km/h. Teraz postanowił podwoić prędkość swojego marszu. Jak długo będzie musiał iść z tą prędkością, aby średnia prędkość całego marszu była równa 5 km/h?

Każda żaba żyjąca na wyspie jest albo zielona, albo niebieska. Po pewnym czasie liczba zielonych żab zmniejszyła się o 60%, a liczba niebieskich żab wzrosła o 60%. Wtedy okazało się, że stosunek liczby żab niebieskich do liczby żab zielonych jest równy początkowemu stosunkowi liczby żab zielonych do liczby żab niebieskich. O ile procent zmieniła się liczba żab na wyspie?

Różnica między największą liczbą trzycyfrową podzielną przez 4 i najmniejszą liczbą trzycyfrową podzielną przez 4 jest równa

Suma wszystkich cyfr pewnej liczby sześciocyfrowej jest parzysta, a iloczyn wszystkich jej cyfr jest nieparzysty. Które ze zdań wypowiedzianych o tej liczbie jest prawdziwe?

Z miejscowości wyruszają co godzinę samochody i jadą tą samą drogą ze stałymi prędkościami. Pierwszy jedzie z prędkością 50 km/h, a każdy następny z prędkością o 1 km/h większą od poprzedniego. Ostatni z nich wyruszył 50 godzin po pierwszym i jedzie z prędkością 100 km/h. Jaka jest prędkość samochodu jadącego na czele kawalkady tych aut po 100 godzinach od momentu startu pierwszego samochodu?

Jaki jest obwód trójkąta, którego wierzchołkami są środki boków trójkąta prostokątnego o przyprostokątnych długości 6 cm i 8 cm?

Gdy Lolek stoi na stole, to jest o 80 cm wyższy od Bolka stojącego na podłodze. Jeśli Bolek stanie na tym samym stole, a Lolek na podłodze, to Bolek będzie wyższy od Lolka o 1 m. Jaką wysokość ma stół?

Żaden z czterech zegarów wiszących w pokoju Marka nie wskazuje poprawnie czasu - każdy z nich albo spieszy się, albo spóźnia się. Czas pokazywany przez pierwszy zegar różni się od czasu właściwego o 2 minuty, przez drugi o 3 minuty, przez trzeci o 4 minuty, a przez czwarty o 5 minut. Pewnego razu Marek, chcąc dowiedzieć się, która jest godzina, odczytał wskazania swoich zegarów: jeden z nich wskazywał za 6 minut trzecią, jeden za 3 minuty trzecią, jeden 2 minuty po trzeciej, jeden 3 minuty po trzeciej. Która była wtedy godzina?

Suma długości trzech boków pewnego prostokąta jest równa 20 cm, a suma długości trzech innych boków tego prostokąta jest równa 22 cm. Ile jest równy obwód tego prostokąta?

W pewnym miesiącu było: 5 poniedziałków, 5 wtorków i 5 śród, a w miesiącu bezpośrednio go poprzedzającym były tylko 4 niedziele. Które ze zdań jest prawdziwe?

A) W następującym bezpośrednio po nim miesiącu będą dokładnie 4 piątki.

B) W następującym bezpośrednio po nim miesiącu będą dokładnie 4 soboty.

C) W następującym bezpośrednio po nim miesiącu będzie 5 niedziel.

D) W następującym bezpośrednio po nim miesiącu będzie 5 śród.

E) Opisana w zadaniu sytuacja jest niemożliwa.

Spośród krawędzi sześcianu wybieramy takie cztery krawędzie, że żadne dwie z nich nie mają wspólnych wierzchołków. Ile jest takich czwórek?

Wczoraj na lekcji matematyki nauczyciel powiedział, że jest to dzień jego urodzin i że iloczyn liczby lat, jakie ukończył i liczby lat, jakie ma jego ojciec, jest równy 2010. W którym roku urodził się nauczyciel?

Ile jest liczb o sumie wszystkich swoich cyfr w zapisie dziesiętnym równej 2010 i iloczynie tych cyfr równym 2?

Ile liczb trzycyfrowych ma tę własność, że środkowa cyfra jest średnią arytmetyczną dwóch cyfr pozostałych?

Magda napisała ciąg liczb, w którym każda liczba, począwszy od trzeciej, była sumą dwóch liczb ją poprzedzających. Czwartą liczbą w tym ciągu była liczba 6, a szóstą 15. Ile była równa siódma liczba w tym ciągu?

Na kartce napisano w jednej linii kilka różnych liczb całkowitych dodatnich nie większych niż 10. Oglądając tę kartkę, Mirek stwierdził ze zdumieniem, że w każdej parze sąsiednich liczb jedna z nich dzieli drugą. Ile co najwyżej liczb mogło być napisanych na tej kartce?

Na płaszczyźnie wprowadzono układ współrzędnych. W początku układu współrzędnych siedzi kangur, który może wykonywać tylko skoki długości 1, przy czym każdy skok jest równoległy do którejś z osi układu. Ile jest punktów płaszczyzny, w których może znaleźć się kangur po wykonaniu dziesięciu skoków?

Jaka jest najmniejsza liczba liter, które należy usunąć ze słowa KANGOUROU, aby otrzymać słowo, w którym litery się nie powtarzają i stoją w kolejności alfabetycznej?

W pudełku jest siedem kart, a na tych kartach są napisane liczby od 1 do 7, każda liczba na innej karcie. Pierwszy Mędrzec wybiera losowo trzy karty z pudełka, a Drugi Mędrzec z pozostałych wybiera losowo dwie. Pierwszy Mędrzec mówi do Drugiego: Wiem, że suma liczb na twoich kartach jest parzysta. Ile jest równa suma liczb na kartach Pierwszego Mędrca?

Ile jest liczb 2008-cyfrowych, których każde dwie kolejne cyfry tworzą liczbę podzielną przez 17 lub przez 23?

W trójkącie ABC punkt D jest środkiem boku AB, punkt E środkiem odcinka DB, a F środkiem boku BC. Jeśli pole trójkąta ABC jest równe 96, to pole trójkąta AEF jest równe

Aby otrzymać liczbę 8⁸, liczbę 4⁴ należy podnieść do potęgi

Wyspę zamieszkują kłamcy i prawdomówni (kłamcy zawsze kłamią, a prawdomówni zawsze mówią prawdę). Pewnego dnia zebrało się 12 wyspiarzy, wśród których byli kłamcy i prawdomówni, i wygłosiło kilka stwierdzeń. Dwóch z nich powiedziało: Dokładnie dwie osoby wśród nas dwunastu to kłamcy. Każda z następnych czterech osób powiedziała: Dokładnie cztery osoby wśród nas dwunastu to kłamcy. Natomiast każda z pozostałych sześciu osób stwierdziła: Dokładnie sześć osób wśród nas dwunastu to kłamcy. Ilu jest kłamców wśród tej dwunastki wyspiarzy?

Iloma zerami kończy się dziesiętny zapis iloczynu kolejnych dziesięciu początkowych liczb pierwszych?

Pudełko czekoladek kosztuje 10 zł. W każdym pudełku znajduje się kupon. Za każde trzy kupony możemy otrzymać dodatkowe pudełko czekoladek gratis. Jaka jest największa liczba pudełek czekoladek, które możemy otrzymać za 150 zł?

Każdą ścianę sześciennej kostki do gry malujemy jednym z dwóch ustalonych kolorów (nie zamalowując oczek). Ile różnych dwukolorowych kostek można w ten sposób otrzymać?

Mama kangurzyca i jej synek Skoczek poruszają się skokami wokół stadionu o obwodzie 330 m. Każde z nich wykonuje jeden skok w czasie jednej sekundy. Skoki mamy kangurzycy mają długość 5 m, a skoki jej synka tylko 2 m. Oba kangury wystartowały jednocześnie z tego samego miejsca i przemieszczają się w tym samym kierunku. Po upływie 25 sekund Skoczek zmęczył się i zatrzymał, a jego mama kontynuowała bieg. Po jakim czasie, licząc od tego momentu, mama dobiegnie do odpoczywającego Skoczka?

W torbie jest 17 kul ponumerowanych liczbami od 1 do 17. Wyjmujemy losowo kule z torby. Jaka jest najmniejsza liczba kul, które należy wyjąć, aby mieć pewność, że wśród nich będzie przynajmniej jedna para kul, których suma numerów jest równa 18?

Rozważamy układy szesnastu różnych dodatnich liczb całkowitych, których średnia arytmetyczna jest równa 16. Największą liczbą, która może wystąpić w takim układzie, jest

Liczby rzeczywiste a i b są różnych znaków. Która z poniższych liczb jest największa?

W okrąg wpisany jest 38-kąt foremny. Kolejne wierzchołki tego wielokąta ponumerowano kolejnymi liczbami od 1 do 38. Jeżeli wierzchołek nr 8 jest jednym końcem średnicy tego okręgu, to drugim końcem tej średnicy jest wierzchołek nr:

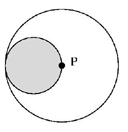Rysunek obok przedstawia dwa styczne koła o stosunku promieni 1:2. Ciemne koło toczy się bez poślizgu po okręgu koła większego. Jaki kształt ma droga przebyta przez punkt P toczącego się okręgu?

W trójkącie ABC miara kąta przy wierzchołku C jest trzy razy większa od miary kąta przy wierzchołku A, a miara kąta przy wierzchołku B jest dwa razy większa niż miara kąta przy wierzchołku A. Trójkąt ABC jest

Gdy baryłka jest w 30% pusta, zawiera o 30 litrów więcej, niż gdy jest w 30% napełniona. Jaka jest pojemność baryłki?

Ile co najwyżej kolejnych liczb całkowitych może mieć te własność, że suma cyfr każdej z nich nie jest podzielna przez 5?

Figura F na płaszczyźnie składa się z 2002 punktów. Prosta l jest osią symetrii tej figury. Dokładnie k spośród punktów figury F należy do prostej l. Której z poniższych wartości nie może przyjmować liczba k?

Na płaszczyźnie ustalony jest trójkąt równoboczny ABC. Ile istnieje wewnątrz tego trójkąta takich punktów X, że pola trójkątów ABX, BCX, ACX są równe?

Litery a i b oznaczają takie liczby całkowite, że wykresy funkcji y=2x+b i y=ax+3 przecinają się z osią Ox w tym samym punkcie. Ile różnych wartości może przyjmować wyrażenie a+b?

Studenci A, B, C, D, E i F stoją w szeregu. Wiadomo, że:

1. D stoi pomiędzy E i F
2. C stoi pomiędzy D i E
3. B stoi pomiędzy C i D
4. A stoi między B i C

Które z poniższych stwierdzeń jest prawdziwe?

O ile procent obniżono cenę kalkulatora, jeżeli po obniżce 5 takich kalkulatorów kosztuje razem tyle, ile 3 przed obniżką?

Trapez ABCD podzielono przekątnymi na 4 trójkąty o polach S₁, S₂, S₃, S₄ (rysunek).
Jeżeli S₂ = 3S₁, to

Piotr rozwiązuje test składający się z 40 pytań. Za każdą poprawną odpowiedź otrzymuje 0,5 punktu, za każdą zaś błędną odpowiedź traci 1 punkt. Piotr odpowiedział na wszystkie pytania i uzyskał łącznie 2 punkty. Na ile pytań odpowiedział poprawnie?

W pokoju znajdowała się pewna liczba osób. Ich średni wiek równy był liczbie osób znajdujących się w pokoju. Gdy do pokoju wszedł 29 letni człowiek, okazało się, że nadal średni wiek był równy liczbie osób w pokoju. Ile osób znajdowało się na początku w pokoju?

Od poniedziałku do środy Marek zawsze kłamie, w pozostałe zaś dni tygodnia mówi prawdę. Pewnego dnia Marek spotkał Marię i powiedział:

1. "Wczoraj kłamałem."
2. "Od pojutrza przez dwa kolejne dni będę kłamał."

W jakim dniu Marek spotkał Marię?

W pewnej rodzinie jest pięć dziewczynek: Ania, Basia, Celina, Danusia i Ela. Rodziły się one w podanej kolejności co 3 lata. Najstarsza Ania jest 7 razy starsza od najmłodszej Eli. Ile lat ma Celina?

Zauważułem że wiek mojej córki pokrywałby się z moim, gdyby w określającej go liczbie cyfry dziesiątek i jedności zamienić rolami. Która z poniższych liczb może wyrażać mój wiek w momencie urodzenia się mojej córki?

Automat matematyczny działa na następującej zasadzie: do danej liczby dodaje 1 lub ją podwaja. Do automatu wprowadzono liczbę 0. Ten po wykonaniu pewnej liczby operacji otrzymał liczbę 100. Jaka jest najmniejsza liczba operacji, którą musi wykonać automat, żeby otrzymać taki wynik?

Na płaskim terenie ustawiono dwa słupy wysokości 3 m i 6 m. Wierzchołek jednego słupa połączono liną z podstawą drugiego słupa i odwrotnie. Na jakiej wysokości krzyżują się obie liny?

Siedmiu grzybiarzy zebrało łącznie 707 grzybów. Okazało się, że każdy zebrał inną ich liczbę, a grzybiarz, który zebrał ich najwięcej, miał o sześć grzybów więcej niż ten, który zebrał ich najmniej. Ile grzybów zebrał rekordzista?

W ciemnej piwnicy jest 20 słoików. Wśród nich jest 8 z dżemem truskawkowym, 7 z dżemem malinowym i 5 z dżemem żurawionwym. Ile co najwyżej słoików można zabrać (po ciemku), aby być pewnym, że w piwnicy pozostaną przynajmniej 4 słoiki jednego rodzaju dżemu i przynajmniej 3 słoiki innego rodzaju dżemu?